2-4-1 星型多角形の内角の和 教材(問題場面) 図のように5つの点A,B,C,D, Eがある。点Aから左回りに1つとば しで点を順に結んでいくと星形五角形 ができる。その内角(∠a~∠e)の和 をいろいろな方法で求めてみよう。 H 活動α3 点が一直線上になる。頂点が内部に入る。 G c ∠a多角形の内角の和/外角の和 n 角形の内角の総和は、多角形の形状に関わらず(凸であれ凹であれ) である。 これはどのような多角形でも、対角線で適当に区切ることで (n2) 個の三角形に分割できることから導かれる。多角形の内角の和 実際に内角の和をだしてみましょう。 N N 角形の内角の和は、 180×(N −2)° 180 × ( N − 2) ° より、 五角形の内角の和は、 180×(5−2) = 540° 180 × ( 5 − 2) = 540 ° 六角形の内角の和は、 180×(6−2) = 7° 180 × ( 6 − 2) = 7 ° 七角形の内角の和は、 180×(7−2) = 900° 180 × ( 7 − 2) = 900 ° となります。 では、なぜこの公式が成立するのでしょうか。 三角形に分割する N N 角形は
五边形内角和怎么求五边形内角度数 天奇生活
多角形内角和
多角形内角和-各内角には2つの外角があるが,外角の大きさというときには,図3に示すようにそのうちの 1つ だけを指す 多角形の外角の和は 360° である 外角を辺に沿って集めると,1点の周りの角になる 1点のまわりの角は 360° であるから,外角の和は 360° になる n角形の 多角形の内角の和、外角を利用した問題です。基本公式をしっかり理解して解いていきましょう。 基本公式 *多角形の外角の和は360°になる 公式を丸暗記するのではなく、公式の導き方を教科書で確認し、自分でも証明できるようにしておいてください。



教师资格面试数学试讲 多边形的内角和 试讲稿 答辩 安徽山香教育
多角形の内角・外角 のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60多边形内角和定理证明 证法一:在n边形内任取一点O,连结O与各个顶点,把n边形分成n个三角形 因为这n个三角形的内角的和等于n·180°,以O为公共顶点的n个角的和是360° 所以n边形的内角和是n·180°2×180°=(n2)·180°(n为边数) 即n边形的内角和等于(n2)×180°(n为边数) 证法二:连结多边形的任一顶点A1与其不相邻的各个顶点的线段,把n边形分成(n2)个三角形多角形の内角の和の公式は180 (n-2)°です。 nは多角形の辺の数が入ります。 三角形の場合n=3なので180 (3-2)°=180°です。 六角形はn=6ですから内角の和=180 (6-2)°=7°です。 考え方は簡単です。 多角形を三角形に分解して考えます。 四角形は2つの三角形に分解できます。 1つの三角形の内角の和は180°ですから四角形の内角の和=180×2=360°です。 今回は
\(n\) 角形の内角の和は \(180^\circ (n − 2)\) であるから、内角の和 \(1260^\circ\) を代入すると \(180^\circ (n − 2) = 1260^\circ\) \(n − 2 = 7\) \(n = 9\) 答え: \(n = 9\) (2) 多角形の外角の和は常に \(360^\circ\) なので、正九角形の \(1\) つの外角の大きさは内角の和は 180°×2=360° となった。 五角形の場合も同じように考えると、 3 つの三角形がで きるので、内角の和は 180°×3=540° 六角形の内角の和は、 180°×4=7° n 角形の場合を考えると、一つの頂点から対角線を引い多角形の内角の和の求め方は: 各頂点において,内角と外角の和は180度。 外角全体の和は,360度。(多角形の外角の和) 凸多角形の場合 (凸と凹) は,それの辺全体と1頂点からひいた対角線全体で,多角形の「三角形分割」が得られます。
三角形の内角の和に始まり,多角形の内角や外角の 和に関する性質は,学校数学の図形教材として馴染み やすい ものの 一 つ である 。 この節では,その組合せ的 性質の特長を整理してみよう 。 (1)三角形の内角の和 「三角形の 内角の和が180eになる 球面の面積は分割された多角形の面積の和であるので冒頭の公式より, S R 2 = \dfrac{S}{R^2}= R 2 S = 全ての内角の和 − ∑ n (n − 2) π c n\displaystyle\sum_{n} (n2)\pi c_n − n ∑ (n − 2) π c n 一つの頂点の周りの角度は球面でも 2 π 2\pi 2 π なので,全ての内角の和は 2 1、内角和:多边形内角和定理 n边形的内角的和等于:(n- 2)×180° 2、外角和:与之对应的是外角,即将其中一条边延长后,延长线与另一条边成的夹角,通常内角外角=180° n边形外角和等于360° 例如:一个多边形的内角和与外角和之比为52,则这个多边形的边数为?



正多边形内角和多边形内角和公式推导方法 尚书坊



教师资格面试数学试讲 多边形的内角和 试讲稿 答辩 安徽山香教育
内角の和が1260°である多角形は何角形ですか、と言う問いに対し、直接1260÷140=9という解答の根拠を教えてください。 数学 締切済 教えて!goo 多角形の内角の和を求める考え方 三角形以上の図形の内角の和は、下表のように補助線を引いて三角形を作り出すことによって理解することができます。 形 図 角度の和 頂点の数 三角形 a b c = 180° 3我们发现五边形内角和也是360°,那么也就是说多边形内角和都是360° 到这里我们就可以证明内角和外角和的规律 多边形内角和,外角和的规律我们也是可以证明的,但我只能用文字来证明。 内角和 在n边形内任取一点O,连结O与各个顶点,把n边形分成n个




多边形内角和 哔哩哔哩 Bilibili



19 1多边形内角和 西瓜视频搜索
多角形の内角の和・外角の和の公式 多角形の内角の和と外角の和の公式をまとめると以下の通り。 N角形の内角の和:180°× (N −2) 180 ° × ( N − 2 ) 多角形の外角の和:360° 360 ° 内角の和は三角形の180°から、角が増えるごとに180°ずつ増えていきます。 それに対し、外角の和は角が増えても変わらず常に360°です。多角形の内角の和中2数学 え、1日27円のプロ家庭教師!? 問題をノーヒントでやってみよう 答えをチェックしよう (1)表は授業動画をご覧ください (2)①1080° ②° (3)①十四角形 ②16本 攻略ポイントを確認しよう ・n角形の内角の和は、180(n-2)で求まる。 ⇒三角形の数で由多角形一个顶点引出的两条边组成的在内部的角,叫作这个多角形的内角。由一边和其相邻的边的延长线组成的角叫作外角。 内角与外角 N角形中,由一个顶点出发,被(n3)条对角线划分出来的三角形个数是(n2)个。那么可以得出n角形的内角和是180°×(n2)。 N角形的外角和可以按照如下方法求。各




不规则多边形内角和公式 搜狗搜索




六角正多边形内角多边形png图片素材免费下载 图片编号 Png素材网
1 正多边形内角和公式 多边形边数公式:n边形的边=(内角和÷180°)2。 此定理适用所有的平面多边形,包括凸多边形和平面凹多边形。 多边形角度公式: 1、n边形外角和等于n·180°- (n-2)·180°=360° 2、多边形的每个内角与它相邻的外角是邻补角,所以n边形内角和加外角和等于n·180° 3、内角正n边形的内角和度数为:(n-2)×180°;正n边形的一个内角是 (n2)×180多角形の内角の和を測ってみよう! 三角形・四角形の内角の和は小学校で習ったと思いますが、それぞれ180°、360°です。 さて、五角形、六角形など、角の数が増えていったら、内角の和はどうなるでしょうか? これを求めるために、三角形の内角が180°というすでに分かっていることを利用することで、わざわざ分度器などを用いなくても知ることが出来ますよ多角形の内角の和 内容 n角形の内角の和は、180°×(n-2)である。 証明A n角形の一つの頂点から対角線を引くとn-3本引けるので、多角形はn-3+1個の三角形ができる。 三角形の内角の和が180°なのでn角形の内角の和は 180°×(n-2)となる。 証明B 多角形の内部に一つの点をとりそこから各頂点に線分を引くと多角形の内部にn個の三角形ができる。



多边形的内角和和外角和 初中数学知识点




怎么求多边形的内角和 百度经验
多角形の内角の和については、以下のように増えていきます。 三角形:内角の和は180° 四角形:内角の和は360° 五角形:内角の和は540° 六角形:内角の和は7° このように、 多角形では辺が一つ増えるごとに内角の和は180増加します。 多角形の和の内角の公式 多角形の内角の和は公式もあります。 角形の内角の和 は何角形かによって変わります。 ・ のとき三角形 ・ のとき四角形 ・ のとき五角形 ・ ・ ・ となっていきます。 実際に計算してみると のとき のとき のとき というようにそれぞれ求めることができます。 多角形の内角の和の公式の説明 多角形の内角の和の公式が となることを説明します。 最初に確認したよ 多角形の内角の和 一覧表と簡単公式による求め方 まず、多角形の内角の和を計算する簡単な公式がこれです。 n角形の内角の和 = 180 × (n – 2) この、 多角形の内角の和についてなるべくシンプル簡単に紹介していきます。 基本的な図形の内角の和は皆さん知っていると思います。 (三角形の内角の和) = 180° (四角形の内角の和) = 360° ここまでは大抵



正多边形内角和公式是什么 初三网




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
次は内角の和から1つ分の大きさを求める方法です。 まず、多角形の内角の和は $$\LARGE{180 \times (n2)}$$ で求めることができましたね。 正三角形の内角の和であれば $$\LARGE{180 \times (32)=180°}$$ 正五角形の内角の和であれば $$\LARGE{180 \times (52)=540°}$$ と求めてやることができます。 内角の和が 同じように五角形の内角の和を考えてみる! 四角形と全く同じやり方で、五角形を三角形に分けてみよう!!こんな感じで↓↓ すると、 緑 の内角の和: 180° 紫 の内角の和: 180° 赤 の内角の和: 180° 緑 紫 赤 の内角の和: 540° ( 180° 180° 180° ) つまり、 正多角形の1つ分の内角は、内角の和を等分することで求めれます。 例 (正三角形) 内角の和180° ⇒ 1つ分の内角\(180\div3=\color{red}{60°}\) (正六角形) 内角の和7° ⇒ 1つ分の内角\(7\div6=\color{red}{1°}\)



多边形内角和公式是什么 初三网




多边形的内角和与外角和 简书
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru还剩 7 页未读, 点击继续阅读 申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。 文档介绍 八年级上数学课件八 多角形の内角の和の公式 そもそも内角とは何なのでしょうか? 内角とは 「多角形の隣り合った二辺が作る、多角形の内側に向いた角」 のことをいいます。 言葉の説明だと、小難しくなってしまうので、三角形・四角形を例に図で説明します。 つまり内角とは、普段私たちが「角度」と読んでいるものの、いわば正式名称みたいなものです。 図に出てき




五边形内角和 五边形的内角和是多少度 52fmz购物网



多边形的角 Kakaisgood 博客园
三角形の内角の和180°を使って多角形の内角の和を考えます。 一つの頂点から他の頂点に補助線を引いて三角形に分けます。 >>クリック 四角形 →三角形2つに分けられる →三角形3つに分けられる 五角形 →三角形4つに分けられる 六角形 四角形の内角の和はは三角形2つ分なので180×2=360 五角形 多角形(三角形、四角形)の内角の和 27 April 16 (三角形の内角の和) = 180° (四角形の内角の和) = 360° 5 5 角形までの内角の和は覚えよう. n n 角形の内角の和は下の公式で求められます. 180 \times (n 2) 180 ×(n − 2) 例えば8角形の内角の和は 180 \times (8 2) = 1080 180 ×(8 − 2) = 1080 と求める. 内角の和から n n 角形の n n を求める これまで 角形の から内角の八年级上数学课件八年级上册数学课件《多边形及其内角和》 人教新课标 (9)_人教新课标 发布 375 kb 35页;



正五边形abcde中 你会求 m的度数吗 陕西中考数学真题 多边形的内角和公式 外角和公式 哔哩哔哩 Bilibili



正多边形内角和多边形内角和公式推导方法 尚书坊
多角形の内角の和 どのような三角形についても,その内角の和は常に $180°$ でした.この事実は一般の多角形についても拡張できます. 多角形の内角の和: $n$ 角形の内角の和は,$180° \times (n2)$ である. 上の事実は次のように説明できます. よって、多角形の内角の和の公式より、正多角形の一つ一つの内角は$$\frac{180°×(n2)}{n}$$と求めることができます。 また、正多角形における外角もすべて等しいため、正多角形の一つ一つの外角も$$\frac{360°}{n}$$と、 和の公式を $n$ で割る ことで求められます。



正方形内角




多边形的内角和 题型的十种解法 星火网校




多边形内角和公式 四年级内角和公式 环球信息网



多边形内角和教案 搜狗图片搜索




在知识迁移 问题类化中探索多角形内角和问题 参考网




多边形的内角



多边形内角和怎么求 百度经验



多边形内角和教学设计 搜狗图片搜索



正多边形内角和公式 高三网



不规则多边形内角和 西瓜视频搜索



五边形的内角和是多少 多边形内角和怎么求 多边形的内角和公式 秦学教育



正多边形内角和 正多边形内角和公式 尚书坊




内角和外角 维基百科 自由的百科全书




多边形的内角和与外角和 简书




内角和外角 维基百科 自由的百科全书



数学长征 多边形内角和 内角和 几何 三角形 四边形



多边形内角和定理在线阅读 沪科版初中数学初二数学下册书 好学电子课本网




多角形の内角の和 は何度なのか を説明します おかわりドリル
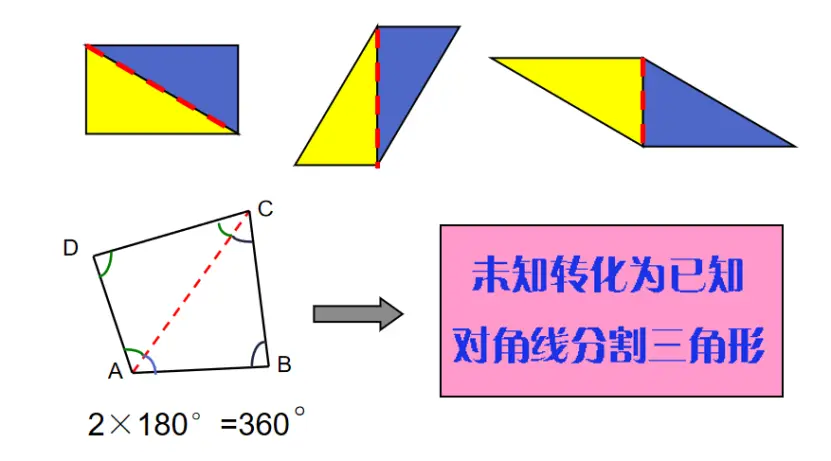



多边形内角和公式的推导 哔哩哔哩




10多边形的内角和进阶平行四边形初中数学初二 Youtube




多边形内角和公式的推导 哔哩哔哩



1 完成表格中未填部分 2 根据表中规律 八边形的内角和是度 3 假设图形的边数为a 内角和为s 请你用一个含有字母的关系式表示图形边数与内角和的关系 S 题目和参考答案 青夏教育精英家教网



多边形内角和 多边形内角和公式 伤感说说吧
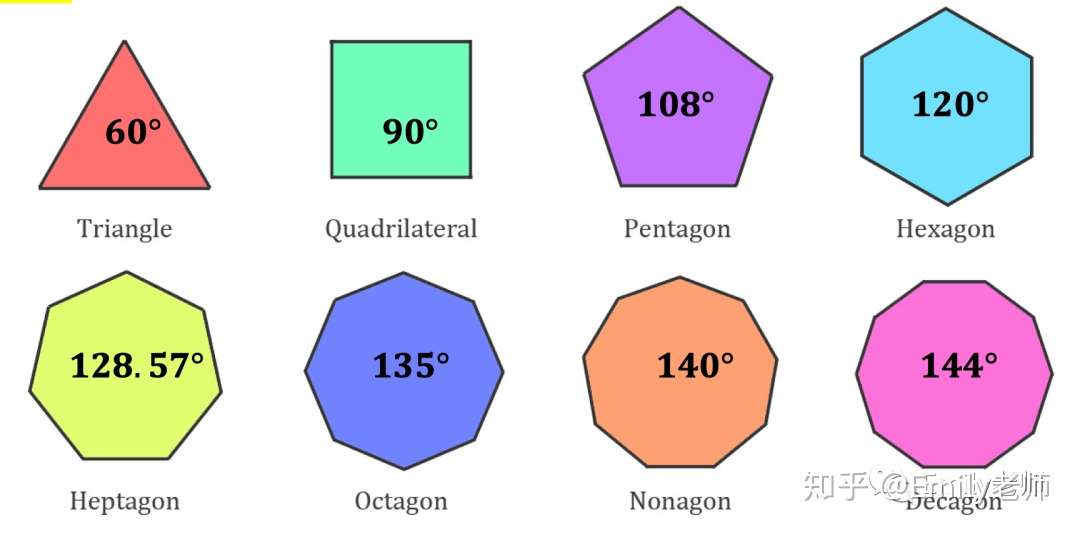



Explore 多边形内角和 知乎




冰姐讲数math Talk 038 解剖多边形内角和的概念 拒绝读死书 反对死读书 阻止读书死 多边形内角和 初中统考 Pt3 Facebook




正多边形 内角 二十角形 十四角 多边形png图片素材免费下载 图片编号 Png素材网



六角形内角和为多少六角形内角和为多少数学 养娃家



2 正多边形的秘密 Python教学视频 李兴球的博客
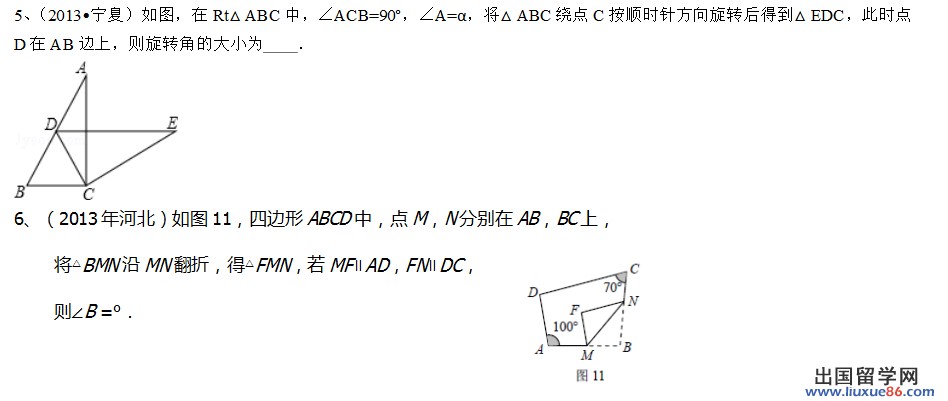



14初三数学三角形多边形内角和外角和



多边形的内角和公式 搜狗图片搜索




11 3 多边形及其内角和6 Ppt




内角の和 180 N 2 外角の和 360 教遊者



头条问答 五边形内角和是多少 好忙碌的回答 0赞




多边形的内角和和外角和 知识点分类总结 学习练习题库 魔分题库



五边形内角和怎么算怎么算五边形内角和 养娃家




多边形内角和怎么求 百度经验




多边形的内角和与外角和题型总结



初中数学多边形内角和 掌握一个公式 学会内外角结合求解边数




多边形的内角



多边形内角和度数 西瓜视频搜索



1



多边形内角和是多少度 初三网



新人教版七下第7 3 多边形及其内角和练习 2 7 3多边形及其内角和 初中人教版 数学中国网



一个多边形的内角和 西瓜视频搜索




22 7 多边形的内角和与外角和八数下冀教版教案 Doc 师客文库



1



多边形一个内角怎么求 初三网
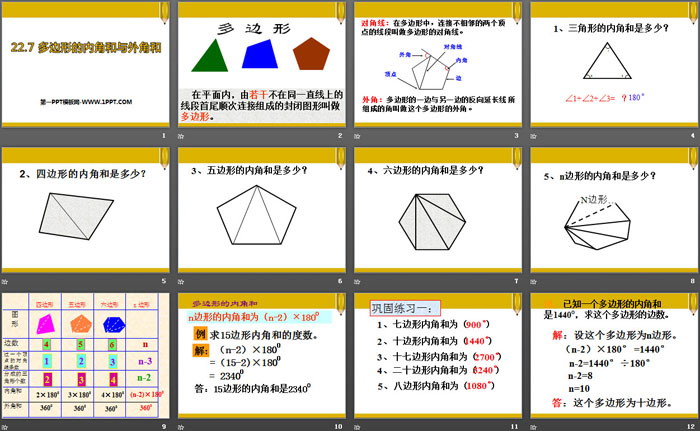



多边形的内角和与外角和 Ppt课件 第一ppt




八年级数学 与多边形的内角有关的计算技巧 会做这四题才算过关 外角 边数 三角形




多边形内角和公式 多边形内角和公式课件 100教育资讯网




乐乐课堂小学数学三年级第99课 多边形内角和 Youtube




多边形内角和和外角和 简书



1




探索多边形的内角和 三角形平行四边形和梯形ppt课件 Ppt课件下载 人人ppt




五边形内角和 五边形的内角和是多少度 52fmz购物网




多边形的内角和 三角形ppt 第一ppt




多边形内角和定理 数学定理 搜狗百科



五边形内角和怎么求五边形内角度数 天奇生活



数学长征 多边形内角和 多边形 内角和 内角 外角



多边形内角和怎么算 扒拉扒拉



如果正多边形的一个内角等于135度那么这个正多边形的边数是 X题卡




多边形内角和 多边形和多边形的内角和 环球信息网




多边形的内角和与外角和 平行四边形ppt 第2课时 第一ppt



初中数学 多边形的内角和 教案



正多边形内角和多边形内角和公式推导方法 尚书坊



课件 教员分享 Z1版 七年级数学 沪教版 八年级下 22 1 探索多边形的内角和 免费数学课件下载 优思教辅




多角形の内角の和 は何度なのか を説明します おかわりドリル



两种解题方法求五边形内角和 知识点需要明晰推导过程进而归纳 每日头条



五边形的内角和是多少 多边形内角和怎么求 多边形的内角和公式 秦学教育




火车过桥 多边形内角和 西安碑林区新曙光培训学校有限公司




星形多边形正多边形内角png图片素材免费下载 图片编号 Png素材网



初中数学多边形内角和 掌握一个公式 学会内外角结合求解边数
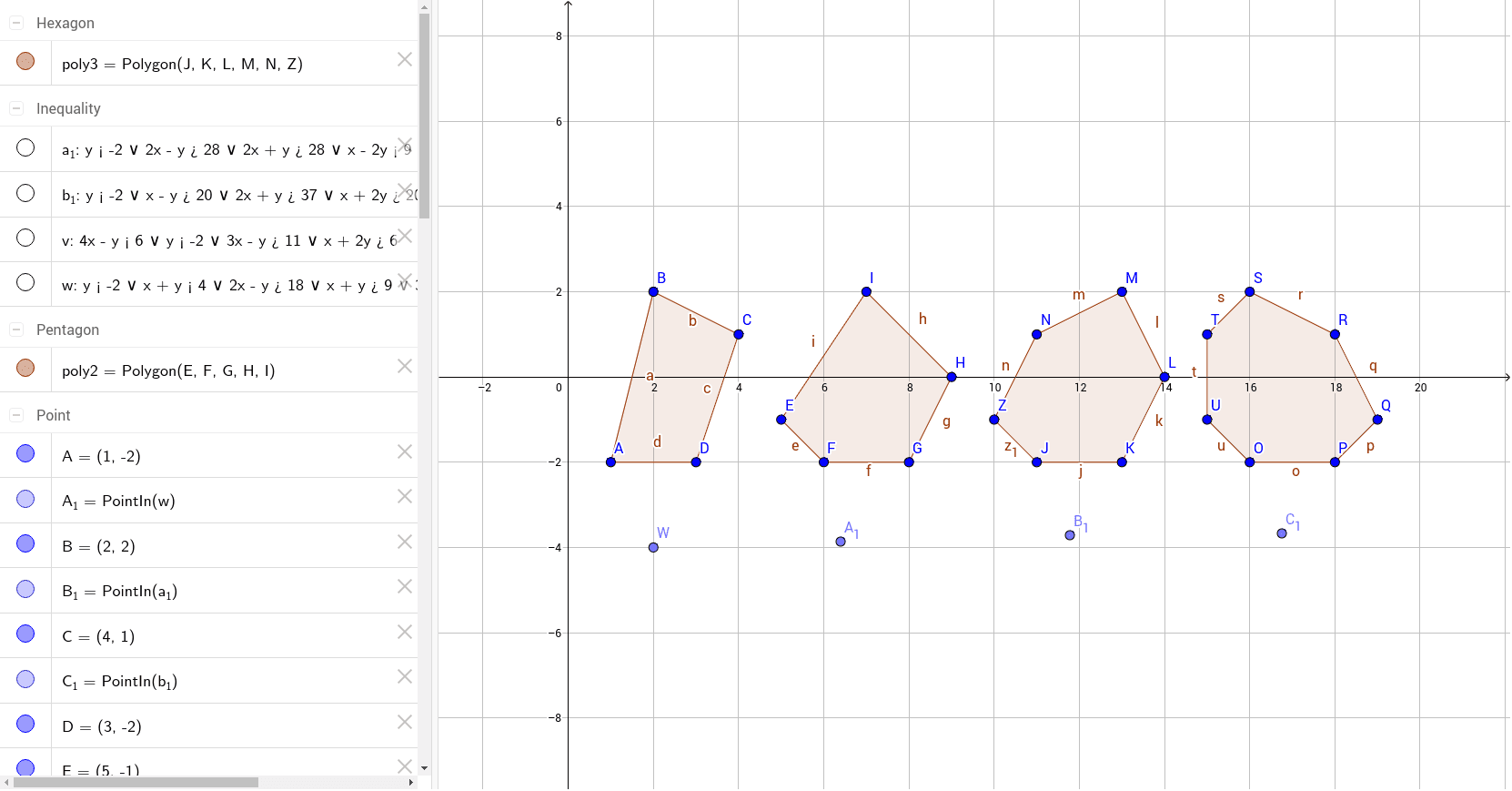



多边形内角和4 Geogebra




正多边形内角和公式及定义 快资讯




多边形内角和与外角和的题型总结



多边形内角和外角 西瓜视频搜索




数学 中2 51 多角形の内角と外角の和 基本編 Youtube



多边形内角和怎么求 百度经验




多边形内角和怎么求 百度经验




在知识迁移 问题类化中探索多角形内角和问题 参考网




多边形的内角和与外角和 简书



多边形内角和外角 西瓜视频搜索
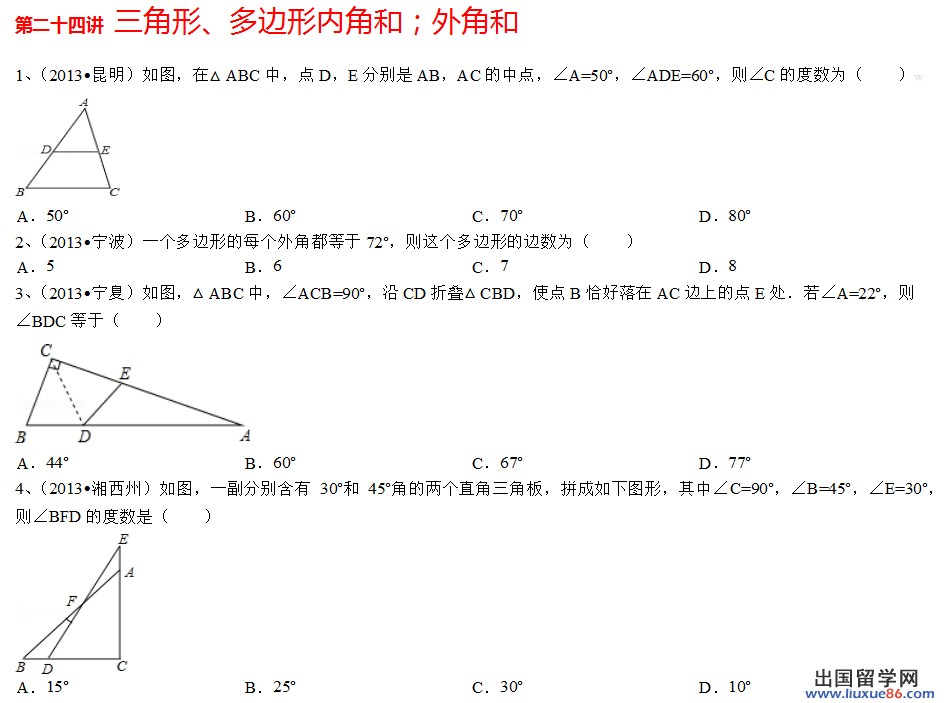



14初三数学三角形多边形内角和外角和




1角形正多边形内角解剖徽章png图片素材免费下载 图片编号 Png素材网




多边形内角和和外角和 简书




七年级数学多边形内角和与外角和 三角形 基础练习 文库吧



多边形内角和外角 西瓜视频搜索




多边形内角和的公式初中数学 多边形的内角和 16教师资格面试真题



0 件のコメント:
コメントを投稿